Optimizing Robot Movement: The Magic of a Well-Tuned PID Controller

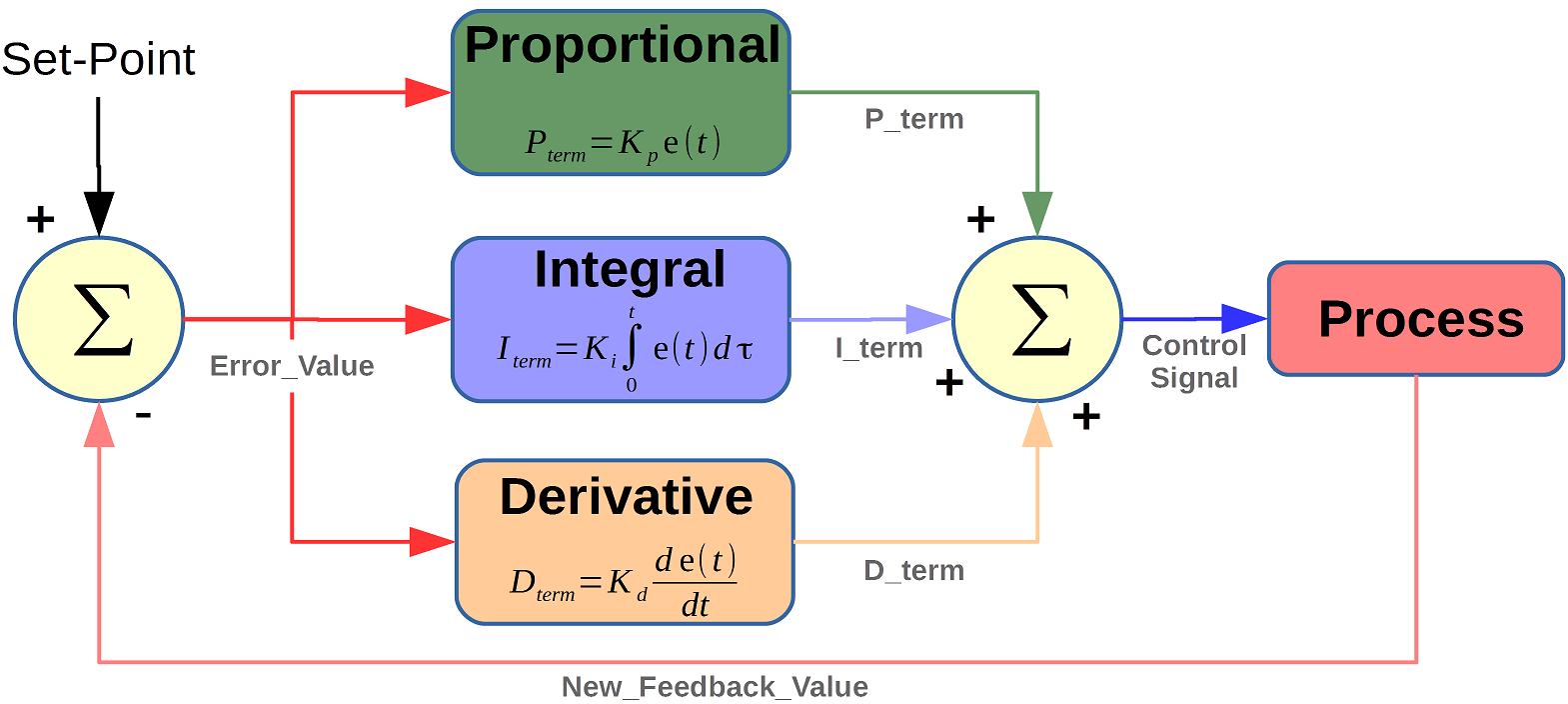
Robots have become an integral part of various industries, from manufacturing to healthcare. Their ability to perform precise and controlled movements is crucial for their efficiency and effectiveness. One of the key players in achieving this precision is the PID controller. In this blog, we'll delve into the world of PID controllers and explore how their careful tuning can significantly impact the movement of a robot around a specific Degree of Freedom (DOF).

Understanding the Basics: What is a PID Controller?

A Proportional-Integral-Derivative (PID) controller is a control loop feedback mechanism that calculates an error value as the difference between a desired setpoint and a measured process variable. It then applies a correction based on proportional, integral, and derivative terms, each contributing to the controller's output.

• Proportional (P) term: This term produces a control response that is proportional to the current error value. A higher proportional gain results in a faster response but might lead to overshooting.
• Integral (I) term: The integral term considers the accumulation of past errors and can help eliminate steady-state errors. It's particularly useful when there's a constant bias.
• Derivative (D) term: The derivative term predicts future errors based on their rate of change. It helps dampen the system's response and prevent overshooting.

The Impact on Robot Movement

Let's consider a robot's movement along a specific Degree of Freedom (DOF), say a robotic arm picking up an object. The goal is to move the arm smoothly and accurately to the desired position. This is where a well-tuned PID controller comes into play.

Without PID Control

In the absence of PID control, the robot's movement might be erratic. It could overshoot the target position or exhibit significant oscillations before settling. This not only affects the efficiency of the task but could also lead to potential collisions or damage.

With PID Control

Now, let's see the difference with a well-tuned PID controller. As the robot starts moving towards the desired position, the proportional term immediately responds to the error (deviation from the setpoint). This quick response reduces the overshooting that could occur. Meanwhile, the integral term gradually eliminates any steady-state error that might be present, ensuring that the robot reaches the exact desired position without any bias. Lastly, the derivative term comes into play to dampen the system's response. It smooths out any sudden changes, preventing oscillations and ensuring a stable and accurate movement.

The Art of Tuning

Tuning a PID controller is an art in itself. It involves finding the right balance between the P, I, and D terms to achieve the desired response. This process often requires a combination of theoretical understanding, experimentation, and fine-tuning.

Visualizing Tuning

The graph above illustrates the tuning process. As the P, I, and D gains are adjusted, you can observe how the response changes. The goal is to minimize settling time, overshoot, and oscillations while maintaining stability.

Conclusion

In the realm of robotics, precision and accuracy are paramount. A well-tuned PID controller can transform a shaky, imprecise movement into a graceful and accurate one. By understanding the interplay between the proportional, integral, and derivative terms, engineers can optimize a robot's movement for any Degree of Freedom, bringing efficiency and reliability to a wide array of applications.

So the next time you see a robot performing a seemingly intricate task flawlessly, remember the unsung hero working behind the scenes: the PID controller.

Remember, the magic is in the tuning!

We hope you enjoyed this exploration of PID controllers in the context of robotic movement. If you have any questions or thoughts, feel free to leave a comment below. Stay tuned for more exciting tech insights!